非绝热载流子动力学理论计算方法

最小面跳跃主要推导过程（Fewest-Switches Surface Hopping, FSSH）

1、哈密顿量

首先定义系统的总哈密顿量$H$：

其中：

• $r$ 代表电子坐标。
• $R$ 代表原子核坐标。
• $H_0(r, R)$ 是原子核固定在位置$R$时的电子哈密顿量（包含电子动能$T_e$、电子-电子势能$V_{ee}$、电子-核势能$V_{ne}$、核-核势能$V_{nn}$）。
• $T_R$ 代表了原子核动能部分。但是由于电子动能是在固定核位置 $R(t)$ 的瞬时情况下求解，原子核的运动由经典轨迹 $R(t)$ 描述，即在电子提供的势能面上经典运动（玻恩-奥本海默近似）。但是，在后续的非绝热耦合项中会出现核速度。因此，核动能的影响已经通过非绝热耦合项包含，而不是显式的 $T_R$。
• 由于原子核动能可以被精确求解，因此将原子核动能提出，其他项作为哈密顿量$H$微扰项处理。需要注意的是，虽然核势能仅依赖核坐标，求解时被视为常数，但是会影响电子态的能量，因此包含在电子哈密顿量中。

2、含时薛定谔方程及电子波函数展开

原子核的运动由经典轨迹 $R(t)$ 描述。因此，电子波函数 $\psi(r, R, t)$ 需要满足含时薛定谔方程：

此时，原子核坐标 $R$ 是时间 $t$ 的函数 $R(t)$。选择一组正交归一的电子基函数 $\phi_j(r; R)$ 来展开总的电子波函数 $\psi$，通常是绝热基函数（此处的展开使用了经典近似，将原子核轨迹当作经典处理，因为原子核的量子波函数特征丢失了，只剩下沿着轨迹演化的展开系数）：

其中：

• $\phi_i(r;R(t))$：是基函数。
• 基函数负责形状，即电子云应该长什么样。但是基函数包含了$R(t)$，当原子核移动时，基函数的形状也随之改变。所以，基函数通过原子核轨迹隐式地依赖于时间。
• $c_i(t)$：是展开系数。模方 $|c_i(t)|^2$ 代表系统处于第 $i$ 个状态的概率。（$c_i(t)$ 是复数，包含实部和虚部）
• 展开系数负责时间演化，其中包含了时间相位，即$e^{-i\int E dt/\hbar}$，后面写相修正的时候应该会再提（如果能写到的话）。
• 物理意义：将复杂的波函数 $\Psi$ 转化为了寻找一组展开系数 $c_i(t)$ 随时间变化的问题。

说明：

• 表象本质上是基函数的选择，是对同一个东西的不同表示。
• 直角坐标系（直角坐标系表象）：用 $(x, y, z)$ 三个数字来描述一个矢量。
• 球坐标系（球坐标系表象）：用 $(r, \theta, \phi)$ 三个数字来描述同一个矢量。
• 虽然给出的基函数： $(x, y, z)$ 和 $(r, \theta, \phi)$ 不同，但是可以表示的是相同的量。
• 在非绝热动力学中，绝热表象 (Adiabatic Representation) 和 透热表象 (Diabatic Representation)是主要选择的两种基函数。
• 一般第一性原理计算软件均采用绝热基函数，计算出的HOMO、LUMO、势能面、能级等均是基于绝热表象定义的。且哈密顿量的对角项即为本征能量，因此物理图像直观。透热基的哈密顿量矩阵不再是对角的，转换较繁琐，这里再不过多涉及。

将展开式（3）带入含时薛定谔方程（2）中，左边可得：

说明：此处使用莱布尼茨法则：$\frac{d}{dx}[f(x)g(x)] = f’(x)g(x) + f(x)g’(x)$

由于$\phi_j(r; R(t))$不显含时间$t$，但是核位置包含时间，因此$\phi_i(r;R(t))$对的时间导数需要使用链式法则进行处理。

说明：

• 链式法则：$\frac{df(g(x))}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx}$
• 为什么$\phi_j(r; R(t))$中电子坐标不含时间$t$：对电子需要使用量子力学处理，如果说$t$时刻电子的位置为$r$，这样描述的电子为经典力学描述。因此，我们只能描述为在$t$时刻，电子在空间中任意一点$r$出现的概率幅是多少。
• 因此，对基函数$\phi_j(r; R(t))$的定义也可以写作：原子核为$R$位置时候，电子云$r$的形状是什么样的。在这个定义中不包含$t$，因为我们只是根据原子核不同位置计算出电子云的形状。所以电子坐标不含时间$t$

展开式（4）可以写作：

其中：

• $\frac{\partial R}{\partial t}$为核速度，即 $\dot{R}$
• $\frac{\partial \phi_j}{\partial R}$为波函数对核坐标的求导，即$\frac{\partial}{\partial x} + \frac{\partial}{\partial y} + \frac{\partial}{\partial z}$，一般情况写作梯度算子$\nabla$
• $\frac{\partial c_j}{\partial t}$一般写作$\dot{c}$，代表概率幅的变化率。

所以整体的展开可以写作：

3、投影

上面得到的为一般情况的式子，但是我们一般不关心全部态，只关心部分态的变化，因此需要对某一个态$k$进行投影，得到态$k$的系数变化率$\dot{c_k}$。

说明：

• 为什么这么做：目前我们的方程中包含了全部的电子态（1，2，3……$j$），无法单独算出态 $k$ 的系数是如何变化的。 例：

• 对于二维空间的一个向量（$c_x$，$c_y$），两个基函数（基向量）分别是$e_x$和$e_y$，向量$V$可以写作$c_x e_x+c_y e_y$。

• 如果我们只关心$e_x$方向上的变化，即我们只想知道$c_x$是如何变化的，需要用$e_x$点乘这个矢量

• 此时得到：$\vec{e}_x \cdot \vec{V} = \vec{e}_x \cdot (c_x \vec{e}_x + c_y \vec{e}_y) = c_x (\vec{e}_x \cdot \vec{e}_x) + c_y (\vec{e}_x \cdot \vec{e}_y)$

• 基向量自己乘自己是1，因此第一项为1。由于$e_x$和$e_y$相互正交，因此第二项为0，这样我们就利用了基向量的正交归一性得到了我们关心的系数$c_x$。

因此，使用同样的方法，在展开式（6）中，左乘$\phi_k^*(r; R)$ 并对电子坐标 $r$ 积分：

说明：

• 后续大部分情况不会再使用积分表达，而使用狄拉克符号，即：$\langle \phi_k |\phi_j \rangle = \int \phi_k^*\phi_j dr$。因此均采用下式：

根据积分的线性性质，即和的积分等于积分的和：$\int [f(x) + g(x)] dx = \int f(x) dx + \int g(x) dx$，可以将求和符号均放在外面，因此展开式（8）变为：

在展开式（9）第二项中，由于$\dot{R}$为核速度，不包含电子坐标，因此可以放在积分外，并且$\dot{c}_j$是关于时间$t$函数，对电子坐标积分为常数，也可以提出积分外。

4、处理展开式

根据前面提到的正交归一性，可以得到$\langle \phi_k |\phi_j \rangle = \delta_{kj}$，如果$k=j$，那么$\delta_{kj}$为1，如果$k\neq j$，那么$\delta_{kj}$为0。

因此展开式（9）的第一项仅保留$k=j$时的$\dot{c}_k$：

展开式（9）的第二项被定义为非绝热耦合矢（Nonadiabatic Coupling Vector, NAC）：

在之前的推导中使用了链式法则，也可以将其还原回去，即：

两种写法都能表示非绝热耦合，是否带有$\dot{R}$需要根据推导情况判定。但是对于使用第一性原理软件和PYXAID软件所进行的数值计算来说，一般采用后一种形式更为方便。（具体原因为后一种形式在数值计算上更为方便，详情见相位修正部分）

注意：

• 在文献当中，非绝热耦合更经常写作：
• $$\frac{\langle \phi_j | \nabla \hat{H} | \phi_k \rangle}{\varepsilon_k - \varepsilon_j} \cdot \dot{\mathbf{R}}$$
• 我们依然从定态薛定谔方程出发，$\hat{H} (r,R) |\phi_k\rangle = \varepsilon_k (R) |\phi_k\rangle$
• 其中 $\hat{H} (r,R)$ 是电子哈密顿量，$\varepsilon_k (R)$ 是本征能量，$|\phi_k\rangle$ 是绝热基函数。其中，电子哈密顿量和电子位置和核位置相关，而$\varepsilon_k (R)$对于电子来说是常数，即本征值，但是对于原子核来说是关于原子核位置$R$的变量，即势能面，所以关于原子核位置的导数需要后续的求导法则进行：
• 对上式求原子核梯度$\nabla_{\mathbf{R}}$：
• $$\nabla_{\mathbf{R}} (\hat{H} (r,R) |\phi_k\rangle) = \nabla_{\mathbf{R}} (\varepsilon_k (R) |\phi_k\rangle)$$
• 应用求导法则：
• $$(\nabla_{\mathbf{R}} \hat{H}) |\phi_k\rangle + \hat{H} (\nabla_{\mathbf{R}} |\phi_k\rangle) = (\nabla_{\mathbf{R}} \varepsilon_k) |\phi_k\rangle + \varepsilon_k (\nabla_{\mathbf{R}} |\phi_k\rangle)$$
• 上面已经说明电子哈密顿量以及本征能量均是关于核位置$R$的变量，因此可以使用求导法则。
• 对上式左乘另一个态 $\langle \phi_j|$
• $$\langle \phi_j | (\nabla \hat{H}) | \phi_k \rangle + \langle \phi_j | \hat{H} | \nabla \phi_k \rangle = \langle \phi_j | (\nabla \varepsilon_k) | \phi_k \rangle + \varepsilon_k \langle \phi_j | \nabla \phi_k \rangle$$
• 第二项化简：哈密顿量是厄密的，即对哈密顿量取复共轭再取转置后等于本身，因此上式第二项可以写作：$\langle \phi_j | \hat{H} | \nabla \phi_k \rangle = \varepsilon_j \langle \phi_j | \nabla \phi_k \rangle$
• 第三项化简：$\nabla \varepsilon_k$对于电子积分来说是一个常数，因为本征能量是哈密顿量的期望值，即：$\varepsilon_k(\mathbf{R}) = \langle \phi_k | \hat{H}{el} | \phi_k \rangle = \int \phi_k^*(\mathbf{r}; \mathbf{R}) \hat{H}{el}(\mathbf{r}; \mathbf{R}) \phi_k(\mathbf{r}; \mathbf{R}) , d\mathbf{r}$，此时已经对电子全空间积分完毕了，因此得到的本征能量只依赖于核坐标$R$，而不再包含电子坐标$r$，因此将$\nabla \varepsilon_k$提取出，根据正交性，这一项为0。
• 化简后：
• $$\langle \phi_j | \nabla \hat{H} | \phi_k \rangle + \varepsilon_j \langle \phi_j | \nabla \phi_k \rangle = \varepsilon_k \langle \phi_j | \nabla \phi_k \rangle$$
• 将含有$\langle \phi_j | \nabla \phi_k \rangle$的项放在一起，整理可得：
• $$(\varepsilon_k - \varepsilon_j) \langle \phi_j | \nabla \phi_k \rangle = \langle \phi_j | \nabla \hat{H} | \phi_k \rangle$$
• 这样就得到了文献中常用的形式： $$\mathbf{d}_{jk} = \langle \phi_j | \nabla_{\mathbf{R}} \phi_k \rangle = \frac{\langle \phi_j | \nabla_{\mathbf{R}} \hat{H} | \phi_k \rangle}{\varepsilon_k - \varepsilon_j}$$

展开式（9）的第三项为电子哈密顿量的矩阵元：

将处理后的三项代回（9）式可得：

我们希望求解的是$\dot{c}_k$，因此将其放在左侧，第二项放在右侧，等式变为：

整理后得：

从式（16）中可以看出，电子态$k$的系数演化$\dot{c}_k$由两项决定：

• 1、$V_{kj}$，电子哈密顿量矩阵元，其物理意义为：当$k=j$时，为$V_{kj}$的对角项$V_{kk}$，代表了在当前的原子核位置 $R$ 下，电子处于态 $k$ 时的本征能量。
• 在绝热表象下，绝热基函数是电子哈密顿量 $H_0$ 的本征函数。因此可以得到其本征方程为： $H_0 \phi_j = E_k \phi_j$ 。
• 左乘$\langle \phi_k$，上式为$V_{kj} = \langle \phi_k | E_j | \phi_j \rangle = E_j \langle \phi_k | \phi_j \rangle = E_j \delta_{kj}$，当$k\neq j$，那么$\delta_{kj}$为0，即所有的非对角元为0。
• 因此，在绝热表象下，这一项为0。
• 
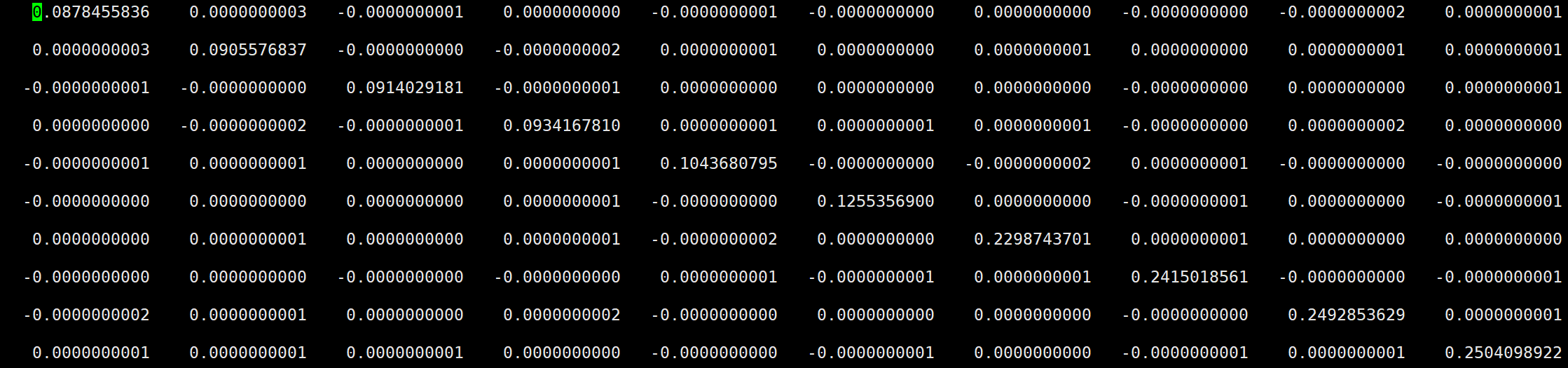
• 如图所示的0_Ham_re文件，对角项为KS轨道的本征能量，非对角项为0。
• 2、$- i\hbar \dot{R} \cdot d_{kj}$，非绝热耦合项，原子核运动越快，或者基函数随位置变化越剧烈，电子态之间的跃迁概率就越大，方向沿着电子云的改变方向。下标的顺序不能随意改变。

5、引入密度矩阵

根据前面的推导可以得到$\dot{c}_k$，但是这个形式只能表示单一态$k$的变化（纯态），且初始条件需要确定。但是一般来说，电子的初始情况是不确定的，可能是纯态，可能是混合态，因此需要引入密度矩阵来讨论更一般的情况。 密度矩阵定义为：

其中：

• 对角元：$a_{kk} = |c_k|^2$ 。这时，密度矩阵和$|c_k|^2$物理含义相同，表示的是态 $k$ 的布居数。
• 非对角元：$a_{kj}$ 表示的是态 $j$ 和 $k$ 之间的相干项（复数）。

例子：

• 波函数$\Psi= c_1\psi1 + c_2\psi2$，计算其$|\Psi|^2$

• $$|\Psi|^2 = \underbrace{|c_1|^2|\psi_1|^2 + |c_2|^2|\psi_2|^2}_{\text{经典概率}} + \underbrace{c_1 c_2^* \psi_1 \psi_2^* + c_1^* c_2 \psi_1^* \psi_2}_{\text{量子耦合}}$$

同样地，我们需要计算密度矩阵$a_{kj}$的概率流$\dot{a}_{kj}$：

上式（18）中出现了系数演化$\dot{c}_k$的复共轭，因此先考虑将式（16）的复共轭写出：

说明：

• 其中，计算非绝热耦合项$d_{jk}$的复共轭为$-d_{kj}$ （即非绝热耦合是反厄密的）
  

证明如下：

考虑$\langle \phi_k |\phi_j \rangle = d_{kj}$，并将$\nabla_R$作用在整体上，得$\nabla_R\langle \phi_k |\phi_j \rangle = 0$。
对整体求导需要分部求导（使用莱布尼茨法则）：$\langle \nabla_R \phi_k | \phi_j \rangle + \langle \phi_k | \nabla_R \phi_j \rangle = 0$
$\langle \nabla_R \phi_k | \phi_j \rangle + d_{jk} = 0$
左边为了将$\nabla_R$放在中间，需要交换内积，取复共轭，即：$\langle A | B \rangle = {\langle B | A \rangle }^$
注意算符作用的波函数不能变，因此$\langle \nabla_R \phi_k |$ 需要整体移动。
因此${\langle \nabla_R \phi_k | \phi_j \rangle}^ = \langle \phi_j | \nabla_R \phi_k \rangle = d_{jk}$
即$d_{jk} + d_{kj} = 0$，故$d_{jk} = -d_{kj}$，证毕。

• 根据以上推导我们可以再证明，如果$k=j$那么$d_{kk} = -d_{kk} = 0$
  
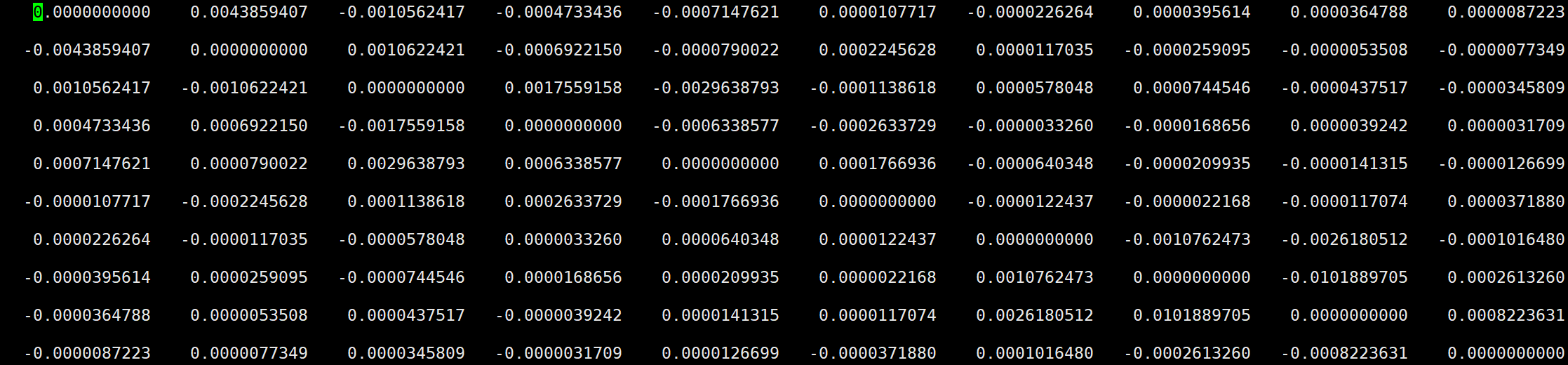
• 如图所示的0_Ham_im文件，对角项为0，非对角项为非绝热耦合项，且对角的非绝热耦合互为相反数。
  

将（16）式和（19）式代入（18），可得：

注意： 由于$j,k$已经表达了不同电子态，因此求和更改符号为$l$，原意不变

将$\frac{1}{i\hbar}$和求和符号全部提出：

其中，$a_{lj} = c_l c_j^$ ，$a_{kl} = c_k c_l^$，因此，上式写为：

说明：

• 电子哈密顿量 $H_{ij}$ 是厄密的，即 $H_{ij} = H_{ji}^*$。（转置取复共轭保持不变）
• 对角项为本征能量，非对角项为非绝热耦合。因为非绝热耦合是反厄密的，所以可以证明哈密顿量是厄密的。

证明如下：

对于仅含有两个态 $1,2$ 的系统，哈密顿量写作：

$$ > H = \begin{pmatrix} > H_{11} & H_{12} \\ > H_{21} & H_{22} > \end{pmatrix} = \begin{pmatrix} > \epsilon_1 & -i\hbar d_{12} \\ > -i\hbar d_{21} & \epsilon_2 > \end{pmatrix} > $$

• 对角元：本征能量 $\epsilon_1, \epsilon_2$ 为实数不变。
• 非对角元：$-i\hbar d_{12}$ 取复共轭后为 $-i\hbar d_{21}$，同理可得另一个非对角元为 $-i\hbar d_{12}$。
• 结论：转置后不变，$H = H^\dagger$，因此哈密顿量是厄密的，证毕。

因此，可以将式（22）中所有的复共轭消除：

首先，我们主要关心布居数 $a_{kk}$ 的变化率。令 $j=k$，上式（23）可以写作：

当$l=k$时，$\dot{a}_{kk}$为0，因此求和只需考虑 $l \neq k$的情况，即：

为了方便，做如下替换：

态 $k$ 布居数的变化率 $\dot{a}{kk}$等于从所有其他态 $l$ 流入态 $k$ 的布居流$b{kl}$之和。
如果$b_{kl}$为正，表示有净流量从 $l$ 流向 $k$。

利用 $a_{lk} = a_{kl}^$ 和 $V_{lk} = V_{kl}^$将上式当中的势能项和非绝热耦合项合并。
1、势能项写作：

这时，如果令$z = a_{kl}^* V_{kl}$，那么$z^* = a_{kl} V_{kl}^$，上式就可以写作： $$ \frac{1}{i\hbar} (z - z^*) \tag{29} $$ 对于任意复数 $z = x + iy$，$z - z^ = (x + iy) - (x - iy) = 2iy = 2i \text{Im}(z)$。
因此，式（29）又可以写作：

将 $z$ 还原为 $a_{kl}^* V_{kl}$，可得势能项写作

注意： 势能项中我们取出的是虚数部分的虚部，而不是虚数，例如$a + bi$中，$a和b$都是实数，$bi$为虚数，但是我们需要的是虚部上的实数，即$b$。

2、非绝热耦合项写作：

类似的，令$z = -i\hbar a_{kl}^* \dot{R} \cdot d_{kl}$，那么$z^* = i\hbar a_{kl} \dot{R} \cdot d_{kl}$，上式就可以写作：

对于任意复数 $z = x + iy$，$z + z^* = (x + iy) + (x - iy) = 2x = 2 \text{Re}(z)$。
因此，式（32）又可以写作：

最终，我们可以将式（27）写作如下形式：

那么，密度矩阵的布居流可以写成如下形式：

而在绝热基下，哈密顿量的非对角元为0，即$V_{kl} = 0$ 因此，最终的$\dot{a}_{kk}$布居数变化仅仅依赖于非绝热耦合的作用，即：

6、如何发生跃迁

如果要实现最小面跳跃，我们需要做出如下约定：

• 1、在发生电子跃迁之前，原子核仅在一个电子态势能面上做经典运动。
  
• 2、允许第$𝑘$个电子态跳跃至其他态$𝑙$ ，并且$𝑘$跳跃至不同$𝑙$是独立的，不允许往返跳跃，以保证跳跃次数最少。
  
• 3、当轨迹足够多时，原子核在$𝑡$时刻处在$𝑘$电子态的比例应等于$𝑎_𝑘𝑘$。
  

N条轨迹

考虑原子核运动共$𝑁$条的经典轨迹（N足够大），在$𝑡$时刻，处在第$𝑘$个电子态上的轨迹数是$𝑁_𝑘(t)$。
此时轨迹分布比例应为体系处于该电子态的布居数，即：

在下一个时刻，即$t+\Delta t$时刻，第$𝑘$个电子态的布居数是$𝑎_{𝑘𝑘} (t+\Delta t)$ 。
我们假定此时在第$𝑘$个电子态的布居数减少，对于经典轨迹来说，处于$k$电子态的轨迹数变少，即$N_k (t)>N_k (t + \Delta t)$此时布居数：

在$\Delta t$时间间隔后，从第$𝑘$个电子态离开的几率为：

其中，单独的$j$态向$k$态跃迁的概率为：

单独的$j$态跃迁概率不一定为正，因此需要判断：

如果后一项小于0，则将这个态的跃迁概率设置为0。
求得所有态向$k$态跃迁概率即为$𝑃_𝑘 (t, \Delta t)$：

因此，从j态向k态的跃迁概率最后可以写作：

判断是否跃迁的随机算法

1、计算所有$g_{kj}$

2、生成$\xi \in [0,1)$的随机数

3、判断是否跃迁

• 若 $\xi < g_{k1}$，则跃迁到态 1；
• 否则若 $\xi < g_{k1} + g_{k2}$，则跃迁到态 2；
• 依此类推，直到找到满足条件的 $j$；
• 若 $\xi > \sum_j g_{kj}$，则保持在当前态 $k$。

能量守恒与速度调整

• 如果发生了跃迁，则需调整原子核速度以保持总能守恒。
• 调整的核速度方向需要沿着非绝热耦合矢（$d_{jk}$）方向。
• 如果动能调整后依然不能满足能量守恒，那么这次跃迁不发生。

含时密度泛函理论下的面跳跃

KS轨道近似

尽管Tully教授提出的FSSH在非绝热动力学模拟中提供了显著的简化，使其能够处理多种电子激发态之间的跃迁。
然而FSSH涉及复杂势能面或者较多电子数时（例如凝聚态系统），依然需要计算多个激发态势能面以及非绝热耦合，这使得计算成本非常高昂。
因此，Oleg教授通过引入科恩-沈吕九（Kohn-Sham, KS）轨道理论对电子态简化处理，并采用经典路径近似，专注描述电子的动力学过程。
之前我们所讨论，电子波函数$\Psi(r,R,t)$是在绝热基函数$\phi_{i}(r;R(t))$上展开的，而我们使用的绝热基函数一般是多电子态的，下面我们需要了解绝热基函数和KS轨道的联系。

我们之前讨论过，整个体系的电子波函数可以由绝热基展开，即公式（3）：$\Psi(r,R,t)=\sum_{i}c_{i}(t)\phi_{i}(r;R(t))$
在这之中，如果整个体系的电子波函数包含$N$个电子，那么每个绝热基函数同样需要包含$N$个电子：

说明：

• 左边的$\Psi$：是一个依赖于$N$个独立变量 $(\mathbf{r}_1, \mathbf{r}_2, …, \mathbf{r}_N)$ 的函数。
• 如果右边某一项$\phi_1$只包含了$(\mathbf{r}_2, …, \mathbf{r}_N)$，那它只是$N-1$个变量的函数。对于变量 $\mathbf{r}_1$而言，它是一个常数。这表明$\mathbf{r}_1$无法描述电子1。
• 左边的$\Psi$的维度为$N$，对于不包含电子1的$\phi_1{r}$，维数为$N-1$，我们无法使用$N-1$维的函数构建出一个$N$维的函数。
• 所有的基函数必须包含完全相同数量的电子。一旦有基函数缺少电子，那么维数为$N-1$无法和$N$维的其他基函数做运算（矩阵、向量计算）。

我们现在了解绝热基函数是多电子态的，接下来需要将多电子态使用单电子基再来描述，即KS轨道，表明KS轨道描述的是单个电子运动的波函数$\varphi_i(r)$

为了描述多电子态绝热基函数 $\Phi_I$ 需要由$N$个选定的单电子态的KS轨道组成的Slater行列式表示。

引入Slater行列式是为了满足以下两点要求： 1、全部电子都是等价的，无法区分。 2、任意交换两个电子，波函数的符号相反，即$\phi (r_1 , r_2)$ = $-\phi (r_2 , r_1)$。（量子力学假定5）

注意：

• 这里说的无法区分指的是可测量的物理量是无法区分的，即$\langle \Psi | \hat{A} | \Psi \rangle$，对于可测量的物理量$A$来说，其测量的期望值 $\left\langle A\right\rangle=\int_{-\infty}^\infty A\left|\Psi(r,t)\right|^2dr$，其中波函数取了平方，符号改变也不会影响$A$的期望值。

为表述方便，我们一般使用$\phi = |\varphi_a(1) \varphi_a(2) \dots \varphi_a(N)|$ 表示多电子的Slater行列式，即：

其中$\frac{1}{\sqrt{N!}}$ 为归一化系数。

考虑一个简单的两电子体系来说，一个在轨道 $\varphi_a$ 上，另一个在轨道 $\varphi_b$ 上。

我们可以写成行列式：

上式也可以写作：

其中每一项的系数为$\frac{1}{\sqrt{2}}$，平方和相加等于1，因此满足概率为1。
如果交换两个电子，式（46）变为：

和式（46）差一个负号。 注意：

• 这里并没有取复共轭，也没有算符，因此$\varphi_a(2)\varphi_b(1)$可以交换顺序。

使用Slater行列式可以极大降低计算量，能够使所有电子的3N维空间积分变成只针对变化的电子的三维积分

• 考虑最简单的两电子体系，此时有三个KS轨道$\varphi_A, \varphi_B, \varphi_C$，它们是正交归一的。
• 初态$\phi_in$，电子占据$\varphi_A$ 和 $\varphi_B$。
• 末态$\phi_out$，电子占据$\varphi_A$ 和 $\varphi_C$。（电子从B轨道跳跃到了C轨道，A不发生改变）
• 此时计算其非绝热耦合，由之前的推导可得非绝热耦合的算符为：$\frac{\partial}{\partial t}$。
• 非绝热耦合算符为单体算符，因此需要对两个电子分别作用，即总的非绝热耦合算符$\hat{O} = \hat{o}(1) + \hat{o}(2)$。其中$\hat{o}(1) = \hat{o}(2) = \frac{\partial}{\partial t}$。
• 因此，总的非绝热耦合$d_{IO} = \langle \phi_{in} | \hat{O} | \phi_{out} \rangle$。
• 我们将初态和末态写成Slater行列式展开： $$ > \phi_{in} = \frac{1}{\sqrt{2}} [\varphi_A(1)\varphi_B(2) - \varphi_B(1)\varphi_A(2)] > $$ $$ > \phi_{out} = \frac{1}{\sqrt{2}} [\varphi_A(1)\varphi_C(2) - \varphi_C(1)\varphi_A(2)] > $$
• 我们可以得到非绝热耦合形式应为： $$ > d_{12} = \langle \phi_{in} | \hat{o}(1) + \hat{o}(2) | \phi_{out} \rangle > $$ $$ > \frac{1}{2} [ \langle \varphi_A(1)\varphi_B(2) | - \langle \varphi_B(1)\varphi_A(2) | ] \hat{o}(1) + \hat{o}(2) | [ | \varphi_A(1)\varphi_C(2) \rangle - | \varphi_C(1)\varphi_A(2) \rangle ] > $$
• 将积分写开会有四项乘积，我们只看第一项即可，其他的均类似。
• 第一项写作： $$ > \langle \varphi_A(1)\varphi_B(2) | \hat{o}(1) + \hat{o}(2) | \varphi_A(1)\varphi_C(2) \rangle > $$
• 其中积分包括两部分，分别对应 $\hat{o}(1)$ 和 $\hat{o}(2)$

• 1、计算 $\hat{o}(1)$： $$ > \iint d r_1 dr_2 [\varphi_A^*(1)\varphi_B^*(2)] \cdot \hat{o}(1) \cdot [\varphi_A(1)\varphi_C(2)] > $$

• 此处，乘法可以交换顺序，除了算符必须作用在它右边的函数上，因此我们把所有关于电子1的放在一起，所有关于电子2的放在一起，重写积分函数 $$ > \iint dr_1 dr_2 \left[ \varphi_A^*(1) \hat{o}(1) \varphi_A(1) \right] \cdot \left[ \varphi_B^*(2) \varphi_C(2) \right] > $$
• 其中算符$\hat{o}(1)$ 只对电子1有作用，关于电子2的函数被视为常数，因此可以移动各项位置，但是要保证$\hat{o}(1)$左侧为$\varphi_A(1)$。
• 接下来使用微积分基本定理：如果被积函数是 $f(x) \cdot g(y)$ 的形式，且积分区域 $x$ 和 $y$ 互不干扰，那么双重积分等于两个单重积分的乘积。 $$ > \iint f(x)g(y) dx dy = \left( \int f(x) dx \right) \cdot \left( \int g(y) dy \right) > $$
• 因此积分又可以写作： $$ > \int dr_2 \left[ \varphi_B^*(r_2) \varphi_C(r_2) \right] \cdot \left( \int dr_1 \varphi_A^*(r_1) \hat{o}(1) \varphi_A(r_1) \right) > $$
• 因为 $\varphi_B$ 和 $\varphi_C$ 是不同的本征轨道，它们互相正交，所以 $\langle \varphi_B | \varphi_C \rangle = \int dr_2 \left[ \varphi_B^*(r_2) \varphi_C(r_2) \right] = 0$，即第一项为0，因此本项为0。

• 2、计算 $\hat{o}(2)$：

• 类似地，积分写作： $$ > \int dr_1 \left[ \varphi_A^*(r_1) \varphi_A(r_1) \right] \cdot \left( \int dr_2 \varphi_B^*(r_2) \hat{o}(2) \varphi_C(r_2) \right) > $$
• 其中第一部分为$\varphi_A$ 自己的重叠积分，即$\langle \varphi_A | \varphi_A \rangle = 1$，因此，这项积分变为单电子积分 $\langle \varphi_B | \hat{o} | \varphi_C \rangle$。
• 第一项为0，第二项仅和两个轨道的单电子积分有关，因此，复杂的多体积分能够转化为简单的单体积分： $$ > d_{IO} = \langle \phi_{in} | \sum_k \hat{o}(k) | \phi_{out} \rangle = \langle \varphi_B | \hat{o} | \varphi_C \rangle > $$
• 这里仅计算第一项，其他项同理。
• 因此，即使行列式不管多么复杂，实际只需要计算单个KS轨道之间的非绝热耦合即可。

以上，为KS轨道和Slater行列式的引入原因。

因此，式（12）所得的非绝热耦合矢 $\langle \phi_k|\frac{\partial}{\partial t}|\phi_j \rangle \cdot$便可以写作两个不同单电子（$p，q$）KS轨道之间的非绝热耦合：

此时，非绝热耦合可以通过数值差分方法求解：

首先，我们将 $t + \Delta t$ 时刻的波函数 $|\varphi_q(t + \Delta t)\rangle$ 在时刻 $t$ 处进行一阶泰勒展开：

上式左乘 $\langle \varphi_p(t)|$：

其中，$O(\Delta t^2)$二阶项极小，因此忽略。并且$\langle \varphi_p(t) | \varphi_q(t)\rangle = 0$，因此忽略。
我们就得到了初步近似：

其中 $\langle \varphi_p(t) | \varphi_q(t+\Delta t)\rangle$ 被称为时间重叠矩阵 (Time-overlap matrix)。
但是上式并不对称，因为有限时间步长会$\Delta t$引入高阶截断误差，从而导致非绝热耦合不是严格反厄密的。因此，使用对称修正解决这个问题。
考虑另一个方向的重叠：

进行类似的展开：

根据式（51）和（52），我们有两个近似式：

• 1、$\Delta t \cdot d_{pq} \approx \langle \varphi_p(t) | \varphi_q(t+\Delta t)\rangle$
• 2、$\Delta t \cdot d_{pq} \approx -\langle \varphi_p(t+\Delta t) | \varphi_q(t)\rangle$ 相加可得： $$ 2\Delta t \cdot d_{pq} \approx \langle \varphi_p(t) | \varphi_q(t+\Delta t)\rangle - \langle \varphi_p(t+\Delta t) | \varphi_q(t)\rangle \tag{55} $$ 现在，我们便求得了$d_{pq}$，将其代入式（36），即电子哈密顿量矩阵元可以写作：$H_{pq} = -i\hbar d_{pq}$，（势能项由于绝热基展开为0）代入上式可得： $$ H_{pq}(t + \frac{dt}{2}) = -i\hbar \frac{\langle \varphi_p(t) | \varphi_q(t+dt) \rangle - \langle \varphi_p(t+dt) | \varphi_q(t) \rangle}{2dt} \tag{56} $$

注意：

• 此处使用的是$\langle \phi_k | \frac{\partial}{\partial t} | \phi_j \rangle$，因此并未出现核速度。
  上式中：
• 分子为不同时刻波函数的重叠矩阵的差。
• 分母来自对称差分的两次时间步长。
• 时刻为$(t + \frac{dt}{2})$表示，计算出的两个时间步的中点，例如计算出$1 fs$和$2 fs$的电子哈密顿矩阵元后，这个数值被认为是$1.5 fs$的数值，以保证数值的稳定性。

经典路径近似（Classical Path Approximation, CPA）

由于凝聚态体系通常较大，电子激发对核运动的影响通常可以被忽略，这就是经典路径近似。
采取经典路径近似表明：

• 1、原子核轨迹是在基态上计算好的，不再随电子态跳跃而改变。
• 2、核速度不再调整，因为轨迹已经固定。

因为不再调整核速度，因此，为了让体系依旧满足细致平衡（Detailed Balance），需要引入玻尔兹曼因子对跳跃概率进行缩放。

说明：

• 细致平衡指在一个描述的是平衡态下的流量守恒。要求从低能态 $k$ 跳到高能态 $j$ 的总流量，必须等于从 $j$ 跳回 $k$ 的总流量。
• 在热平衡下，状态的概率由玻尔兹曼分布给出： $$ \frac{P_k}{P_j}=\frac{e^{-E_i/k_BT}}{e^{-E_j/k_BT}}=e^{(E_j-E_k)/k_BT} $$
• 采用CPA后，原子核不再对电子能量的变化做出反应。而在标准FSSH中，向上跃迁（吸收能量）需要原子核动能改变以保证总能量守恒，如果动能改变不足以支付跃迁的能垒，就不会跳跃，从而维持平衡。
• CPA以后，相当于向上跃迁不再需要能垒，因此，向上跃迁（吸收能量）和向下跃迁（放出能量）将由同样的耦合强度驱动，概率几乎相等。这将导致长时间的演化后，计算出的所有态会有相同的布居数，即$\frac{P_k}{P_j}$ = 1。在上式中，对应于$T = \infty$，因此，需要使用玻尔兹曼因子对向上跃迁进行抑制。

修正后的跃迁概率公式：

如果是向下跃迁：

表明向下跃迁（放出能量）不会受到限制。 如果是向上跃迁：

表明向上跃迁（吸收能量）被指数抑制，抑制程度取决于能级差和温度。

量子退相干修正

在量子系统的独立演化过程中，若无外界干扰，量子态之间的相干性能够保持。但当系统受到外部扰动时，量子叠加态会被破坏，导致波函数分支和相位分离，使体系迅速坍缩至某一量子态，即发生退相干。
但是，混合量子-经典的FSSH方法将量子态分叉、相干演化与核波包传播替换成 ‘经典轨迹 + 随机跳跃’。
在全量子方法中，电子与原子核均进行量子化处理，体系波函数能够保持良好地相干性质。
但是在FSSH方法中，电子被量子化地处理，而原子核采用经典描述，电子与核波函数之间的量子耦合作用无法被正确地描述，因而天然地具有退相干缺失的算法缺陷。
因此，FSSH无法严格满足量子理论对动量、布居数和相干性的要求。

一般来说，我们认为在CPA-FSSH量子-经典混合动力学方法中天然地具有过度相干的问题，这主要来自于以下三个方面：

• 1、CPA近似导致原子核轨迹并未依照非绝热跃迁发生分支，电子波函数的相干演化被保持过久，即使已经发生跃迁，电子波函数仍保留之前轨道的信息，核轨迹之间的相干没有被及时破坏引发过度相干。
• 2、FSSH算法通过概率公式决定是否发生跳跃的，即式（43）：
• $$P_{j \to k} = \frac{2 \text{Re}(c_j^* c_k d_{jk} \cdot \mathbf{v})}{|c_j|^2} \Delta t $$
• 假设已经发生了跃迁，即由j态跃迁到了k态，但是电子的波函数的系数并没有随之坍缩，而是继续连续演化。也就是说，系数 $c_j$ 和 $c_k$ 的数值不会发生突变，依然保留了跳跃前的数值，并继续平滑演变。这样会导致对于原子核部分来说系统已经完全处于跳跃后的k态了，但是电子依然是j态和k态的混合态，违背了量子测量的坍缩原理（测量假设）。在使用上式计算概率时，通常会给$c_j$一个极小值，这使得电子始终处于多态叠加的状态，而不是单一明确的状态，从而引入了非物理的过度相干。
• 3、通常我们采用一系列不同的初始条件，形成大量跃迁轨迹的系综，并对系综平均尝试人为地引入不确定度，从而重构量子效应。但这种方法获得的轨迹间的相位关系仍然被保留，不同轨迹之间存在高度相似的演化过程，仍然无法有效引入退相干。

说明：

• 如果电子处于两个态，例如基态Groud State和激发态Exctied State的叠加时，我们可以把波函数写作如下形式：
• $$\varphi = c_{k} \phi_{k} + c_{j} \phi_{j}$$
• 这里的系数 $c$ 是复数，可以将模和相位分开表示：$c_k = |c_k|e^{i\theta_k}, c_j = |c_j|e^{i\theta_j}$。
• 相位差就是$\Delta \theta = \theta_k - \theta_j$。
• 根据式（17）下的例子，我们引入的密度矩阵中，密度矩阵的非对角元体现了相干性，这里考虑非对角元其中一项：
• $$ c_k c_j^* = |c_k||c_j| e^{i(\theta_k - \theta_j)}$$
• 只要$c_k c_j^* \neq 0$，那么这两个态就存在相位关系，就具有相干性，能够发生量子干涉。
• 但是，在统计平均下，相位差是完全随机的，有是相位差是$0°$ （$e^{i0} = 1$），有时是$180°$（$e^{i\pi} = -1$），这就导致在时间平均下，$c_k c_j^* \to 0$。此时两个态失去了量子相干性，导致退相干，此时量子概率变成了经典轨迹，这是量子测量的基本假设所决定的。

尽管存在**退相干诱导表面跳跃（Decoherence-Induced Surface Hopping, DISH）**等方案能够在面跳跃过程中显式地引入退相干和态坍缩过程，但其结果仍是近似的。不过对于目前的计算资源限制来说，CPA+DISH修正依然是一座无法逾越的大山。

随机演化算符

在DISH方法中，首先定义了复合时间演化算符 $\tilde{\hat{U}}(t, t_0)$，并引入一个退相干算符$\hat{L}_{\alpha}(t)$和标准含时薛定谔方程演化算符$\hat{U}(t, t_0)$，其中复合时间演化算符定义为：

其中：

• $\hat{U}(t, t_0)$：代表标准的含时薛定谔方程演化，产生相干的量子叠加态。
• $\hat{L}_{\alpha}(t)$：代表退相干算符，它随机地将波函数“定位”或“坍缩”到某个绝热基态上。

时间演化算符：

• 在和外界没有任何相互作用的孤立系统中，波函数的演化严格遵循含时薛定谔方程，即式（2）：
• $$i\hbar \frac{\partial}{\partial t} |\psi(t)\rangle = \hat{H} |\psi(t)\rangle$$
• 定义的时间演化算符$\hat{U}(t, t_0)$作用在$\partial t$上能够把波函数从$t_0$时刻转移到$t$时刻，即：
• $$|\psi(t)\rangle = \hat{U}(t, t_0) |\psi(t_0)\rangle$$
• 需要注意的是，含时薛定谔方程是微分方程，其描述的是波函数在某一时刻$t$的变化率。但是时间演化算符是积分形式，描述的是波函数在到$t$时刻会变成什么样子。特别是在数值模拟中，我们已知初始状态$\psi(t)$以后，含时薛定谔方程给了我们这个波函数如何变化，但是时间演化算法才能直接计算出下一刻位置波函数的样子$\psi(t_0)$
• 我们将时间演化算符代入含时薛定谔方程中，得到：
• $$i\hbar \frac{\partial}{\partial t} \left( \hat{U}(t, t_0) |\psi(t_0)\rangle \right) = \hat{H} \left( \hat{U}(t, t_0) |\psi(t_0)\rangle \right)$$
• 此时，我们得到的波函数$\psi(t_0)$已经是在$t_0$时刻的波函数了，此时这个波函数是定态的，与时间无关，因此两边可以直接把$\psi(t_0)$约掉，得到算符的微分方程：
• $$i\hbar \frac{d}{dt} \hat{U}(t, t_0) = \hat{H} \hat{U}(t, t_0)$$
• 把常数移到右边可得：
• $$\frac{d}{dt} \hat{U}(t, t_0) = -\frac{i}{\hbar} \hat{H} \hat{U}(t, t_0)$$
• 我们可以看到，算符$\hat{U}(t, t_0)$在求导后等于它本身，因此，我们可以认为它的解是一个$e$指数形式：
• $$\hat{U}(t, t_0) = e^{-i\hat{H}(t - t_0)/\hbar}$$
• 时间演化算符属于幺正算符，即$\hat{U}^* \hat{U} = \hat{U} \hat{U}^* = \hat{I}$。其中，$\hat{I}$为单位算符。将时间演化算符作用在波函数上以后，只改变波函数的方向（相位）而不改变大小（模长）。这种演化会长时间保持系统的相干性。因此，我们需要在时间演化算符作用下，让波函数在有相干性的动力学过程中发生演化，再由退相干算符介入，打破相干性，从而使用这两个算符实现退相干。

退相干算符：

• 退相干算符$\hat{L}_{k}(t)$是一个随机算符，其具体形式取决于一个均匀分布的随机数 $\zeta \in [0, 1]$ 与当前量子态在态 $k$ 上的概率 $|c_k|^2$ 的比较结果，其定义如下：
• $$\hat{L}_{k}(t) =\begin{cases}\frac{\hat{P}_{k}}{|| \hat{P}_{k} |\psi\rangle ||} & \text{如果 } \zeta \le |c_{k}|^2 \quad (\text{坍缩到态k} ) \\\frac{\hat{I} - \hat{P}_{k}}{|| (\hat{I} - \hat{P}_{k}) |\psi\rangle ||} & \text{如果 } \zeta > |c_{k}|^2 \quad (\text{将态k投影出去，使其不再存在在波函数中})\end{cases}$$
• 其中$\hat{P}{k} = |\phi{k}\rangle\langle\phi_{k}|$ 是向绝热基态 $k$ 的投影算符。分母就为归一化因子，确保作用后波函数的模长为1。
• 在之前的推导中，我们提到过需要将态进行投影从而得到得到某个态的系数变化率。但是这里，我们需要的是演化后的一个新的态，而不是数值，因此我们需要使用投影算符$\hat{P}{k} = |\phi{k}\rangle\langle\phi_{k}|$将其作用在一个态上，才能产生一个新的态。例如：
• 假设$|\psi\rangle = c_1 |\phi_1\rangle + c_2 \phi_2\rangle|$，将投影算符$\hat{P}_1 = |\phi_1\rangle\langle\phi_1|$作用在上面
• $$\hat{P}_1 |\psi\rangle = (|\phi_1\rangle\langle\phi_1|) |\psi\rangle = c_1 |\phi_1\rangle$$
• 这样，我们就通过投影算符得到了一个新的波函数，这个波函数保留了原来的振幅信息 $c_1$，但方向被强行改变到了基函数 $|\phi_1\rangle$ 的方向上。这正是“波函数坍缩”的数学定义。
• 但是随之而来的问题是，在投影到 $|\phi_1\rangle$ 方向之后，概率不再守恒。例如：
• 波函数为 $|\psi\rangle = 0.6|\phi_1\rangle + 0.8|\phi_2\rangle$，此时总概率为$|0.6|^2 + |0.8|^2 = 0.36 + 0.64 = 1$。在不归一化的情况下使用投影算符$\hat{P}_1 = |\phi_1\rangle\langle\phi_1|$后：
• $$|\psi\rangle = \hat{P}_1 |\psi\rangle = 0.6|\phi_1\rangle$$
• 此时新波函数的模长平方是 $|0.6|^2 = 0.36$。这意味着粒子只剩下 36% 的概率存在，另外 64% 的粒子凭空消失了，因此，这时候除以模长0.6后，才能使得新波函数在$|\phi_1\rangle$的概率为1。
• 退相干算符不是幺正算符，因此上式才使用归一化。它会随机将波函数坍缩到某个绝热基态上。
• 上面投影算符的式子表明，如果随机数小于概率$\zeta \le |c_{k}|^2 \quad$，那么投影算符作用在波函数上，导致波函数变为纯态 $\psi = \phi_k$，不再和其他态存在相干性。如果$\zeta > |c_{k}|^2 \quad$，则将态k从投影出去，使其不再存在于波函数中，轨迹会根据剩余态的相对概率跳跃到其他的某个态上（因为此时我们已经得知此时不在k态上，因此为了符合测量导致态发生坍缩的投影假设，波函数中属于态k的成分必须消失）。

退相干时间

DISH需要计算退相干时间从而判断叠加态能维持多久，退相干时间由下式决定：

其中：

• 1、$r_{kj}$：是态 $k$ 和态 $j$ 之间的纯去相速率，可以由光学响应理论或冻结高斯近似等公式预先计算或在线计算。
• 2、$|c_i(t)|^2$：是其他态的布居数。 式（61）代表了，如果波函数主要处于态k上，那么其他态的布居数接近0，此时退相干时间接近$\infty$，此时能够一直稳定在态k上，如果其他态叠加程度高，退相干则发生的越快。

纯去相速率使用光学响应理论表示。计算可以得到光学响应函数，或者叫得更熟悉一点——重叠积分$J_{jk}(t)$。重叠积分的模值衰减速率就是纯去相速率。

注意：

• 我们一般说的$\langle \psi_j | \psi_k \rangle = 0$指的是同一时刻，统一哈密顿量下的电子基函数是正交的。上面的重叠积分描述的是同一个态在两个势能面上演化的重叠程度，或者说是原子核在势能面k和势能面j上演化，在时间t时，两个态长得有多像。 式（62）一般采用CPA后进行统计平均，一般来说，这两个波函数在一开始会处于同一个初态$\psi_0 \rangle$，然后随时间演化后发生态之间的跃迁： $$ J_{jk}(t) = \langle \psi_j(t) | \psi_k(t) \rangle = \langle \psi_0 | e^{i\hat{H}_j t / \hbar} e^{-i\hat{H}_k t / \hbar} | \psi_0 \rangle \tag{63} $$ 其中 $\hat{H}j$ 是当电子处于态 $j$ 时的原子核哈密顿量（动能和势能），因为$J{jk}(t)$描述的是原子核在不同位置的重叠程度，因此这里是原子核的哈密顿量。 在CPA近似下，式（63）中的原子核哈密顿量算符可以直接得到具体的数值，因为核轨迹$R(t)$ 已经被确定了，因此可以直接替换成某一时刻的标量函数，即 $$ \hat{H}_k \approx E_k(R(t)) \tag{64} $$ 因此，式（63）可以替换为： $$ e^{-i\hat{H}_k t / \hbar} \rightarrow \exp\left[ -\frac{i}{\hbar} \int_0^t E_k(\mathbf{R}(\tau)) d\tau \right] \cdot \langle \psi_0 | \psi_0 \rangle \tag{65} $$ 将式（65）代入式（63）中，可得： $$ J_{jk}(t) \approx \left\langle \exp\left[ \frac{i}{\hbar} \int_0^t E_j(\tau) d\tau \right] \exp\left[ -\frac{i}{\hbar} \int_0^t E_k(\tau) d\tau \right] \right\rangle \tag{66} $$ $$ J_{jk}(t) \approx \left\langle \exp\left[ -\frac{i}{\hbar} \int_0^t \left( E_k(\tau) - E_j(\tau) \right) d\tau \right] \right\rangle \tag{67} $$ 令$\Delta E_{jk}(\tau) = E_k(\tau) - E_j(\tau)$ ，那么 $$ J_{jk}(t) \approx \left\langle \exp\left[ -\frac{i}{\hbar} \int_{0}^{t} \Delta E_{jk}(\tau) d\tau \right] \right\rangle_T \tag{68} $$ 因为我们需要对大量初始位置和动量平均，因此引入了外面的尖括号 $\langle \dots \rangle_T$，表示对多条轨迹取平均。 但是上式计算依旧复杂，通常使用二阶累积量展开近似。 首先计算两条电子态之间的能级差$\Delta E_{jk}$相对于平均值的涨落： $$ \delta U(t) = \Delta E_{ij}(t) - \langle \Delta E_{ij} \rangle \tag{69} $$ 然后计算能隙涨落的非归一化自相关函数（Unnormalized Autocorrelation Function, unACF）： $$ C_{un}(t) = \langle \delta U(t) \delta U(0) \rangle \tag{70} $$ 上式反映的是环境对电子的能级位置影响持续多久，通常会随时间衰减。
  将自相关函数进行双重时间积分，直接得到响应函数的衰减形式 ： $$ J_{jk}(t) \approx \exp\left[ - \frac{1}{\hbar^2} \int_{0}^{t} d\tau_2 \int_{0}^{\tau_2} d\tau_1 \langle \delta U(\tau_1) \delta U(0) \rangle \right] \tag{71} $$ t字母在之前使用过，因此使用$\tau$更换积分上限。
  现在我们获得了$J_{jk}(t)$，求高斯拟合便可以获得纯去相速率。这种方法将复杂的量子相互作用的环境使用能级差来表示。
  最后，我们将得到的纯去相速率代回（61），便能得到退相干时间。

随机判断退相干事件

在DISH方法中，使用泊松过程来判断是否退相干。
首先根据之前的步骤计算退相干时间，设为$\tau_{k}$，它代表了在当前环境下，态 $k$ 平均能维持多久的相干性。
生成一个随机数$T$，代表在这次随机当中，允许叠加态存活的时间。
如果当前时间演化算符所演化的时间（距离上一次退相干过去的时间）超过了随机生成的寿命，那么立刻使用退相干算符对波函数进行坍缩或者投影移除态k，这就是DISH算法中发生跃迁的时刻。
如果没有超过，那么波函数继续根据时间演化算符进行演化，到下一个时间步长再判断。
这两种结果取决于量子概率 $|c_{k}|^2$：

• 1、坍缩到k态，概率为$|c_{k}|^2$，这时波函数变为纯态$\psi = \phi_k$，如果当前势能面不为k态的势能面，则发生跳跃，跳到k态势能面上。
• 2、将k态投影出去，概率为$1 - |c_{k}|^2$，态k的系数设置为0，波函数在剩余态中重新归一化。如果这时当前势能面为k态的势能面，但是k态被投影出去了，则必须跳跃到其他态上，跳跃到哪个态上根据剩下态归一化以后相对的概率分布决定。

结论

至此，基本的非绝热载流子动力学理论方法我们就推导完毕了，尽管FSSH依然是“经典+量子”处理载流子跃迁，例如使用随机数判断是否发生跃迁，以及对动量进行调整，并且最小面跳跃会将跃迁简化，无法严格满足量子理论对布居数、动量和退相干的一致性条件，但是也是目前能够使用的较为方便的计算载流子寿命的方法。后续会介绍的泊松化量子动力学则使量子动力学遵循严格的数学推导并重现量子系统信息，在不讨论原子核量子化的情况下，提供了一种严格量子一致、物理图像清晰、跃迁统计可控的非绝热动力学路径采样框架。

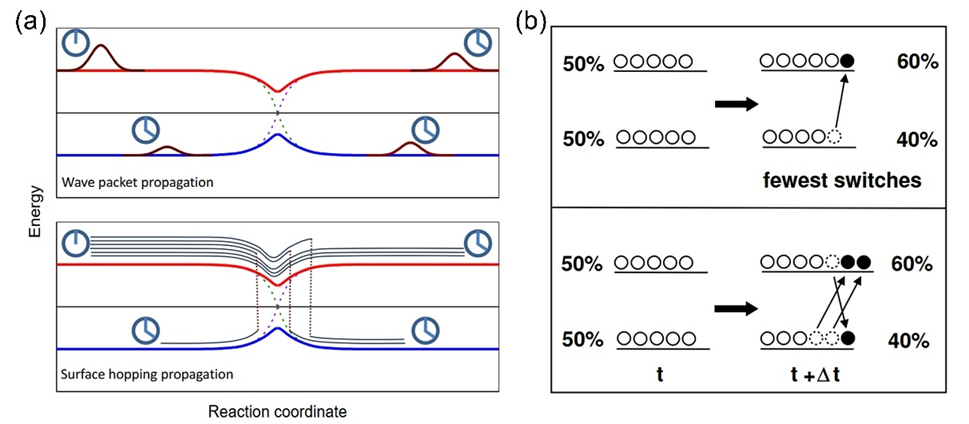
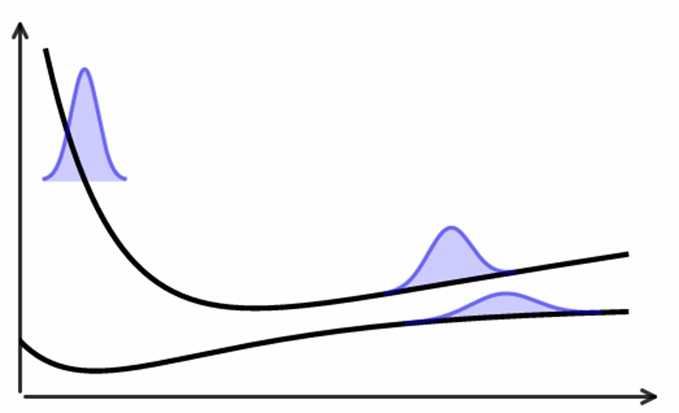
如图所示，图（a）为简单避免交叉势能面，在耦合区域随着时间推移应该会多次跃迁。
图（b）为FSSH和实际跃迁的差别，本应该跃迁三次的粒子，FSSH将其简化成了一次。

PYXAID设置

PYXAID主要编写为C++，通过python字典传递参数。

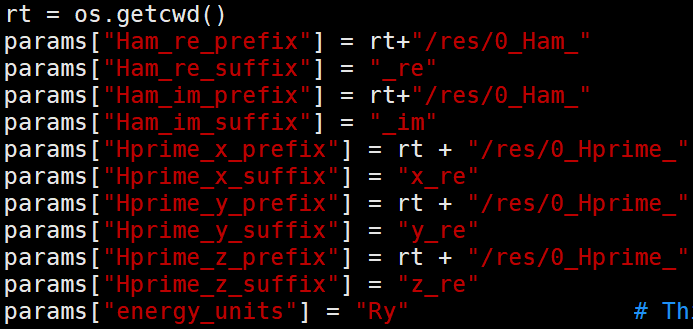
上面这段参数主要读取哈密顿量文件，以及其单位，这里设置成Ry是因为在从real文件转换成哈密顿量文件的时候进行了单位转换。哈密顿量文件实部（0_Ham_xx_re）中保存的对角元就是KS轨道的能量，单位为Ry。Hprime则对应跃迁偶极矩，如果包含激光激发，则需要使用，这里不涉及。

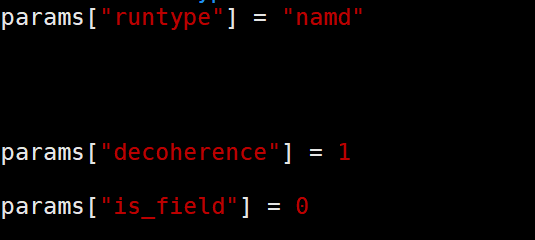
params[“runtype”] = “namd”，设置为namd为执行动力学演化，设置为no-namd不跑动力学，仅检查基组能量。
params[“decoherence”] = 1，表示是否使用DISH方法校正。设置为0表示标准FSSH，不包含退相干，此时只有时间演化算符 $\hat{U}$ 演化，没有退相干算符 $\hat{L}$ 介入。设置为1表示开始DISH计算，此时会计算退相干时间，并引入退相干算符 $\hat{L}$。
params[“is_field”] = 0，表示是否包含光场激发。0不包含，1包含，如果包含，则会在玻尔兹曼因子分母上引入一个光子能量。

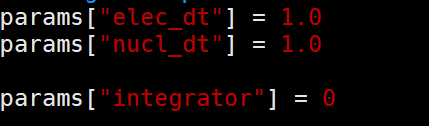
params[“elec_dt”] = 1.0，表示电子积分的时间步长。
params[“nucl_dt”] = 1.0，表示核积分的时间步长，必须和哈密顿量文件产生时的时间步长保持一致。
params[“integrator”] = 0，用什么方法计算积分。

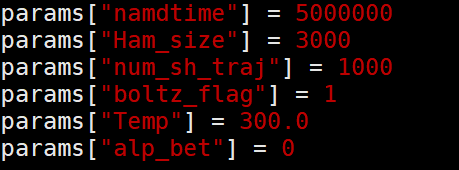
params[“namdtime”] = 5000000，表示模拟namd的总时长，5ns。
params[“Ham_size”] = 3000，表示有多少个哈密顿量文件，如果不足以覆盖上面的总时长，PYXAID会自行把哈密顿量进行ABCDABCD首尾相接以补充足够，例如这里仅3000个哈密顿量文件，PYXAID会补充到上面的5ns。设置太长会导致计算量过大，PYXAID无法运行。
params[“num_sh_traj”] = 1000，表示使用多少个轨迹进行平均，这里为总轨迹数$N$，如果处于$k$态的轨迹数为300，那么此时算出来的跃迁概率就为0.3，设置300-500均可，设置过多会导致计算量较大。这里是采样的电子的量子跳跃概率，它表示了：对于完全相同的原子核初始构型和运动路径，程序会重置随机数种子，尝试1000次不同的跳跃可能来判断电子处于$k$态的概率是多少。
params[“boltz_flag”] = 1，使用玻尔兹曼因子对向上跃迁的概率进行缩放，如式（58）、（59）所示，必须打开。
params[“Temp”] = 300.0，使用玻尔兹曼因子缩放时的温度。
params[“alp_bet”] = 0，是否考虑自旋耦合，后续再补。

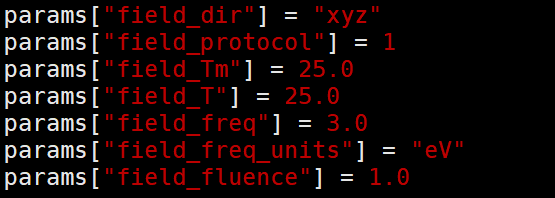
上图均为设置的光场参数，暂不考虑。

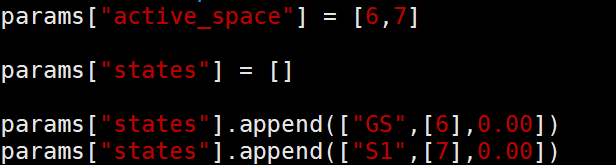
params[“active_space”] = [6,7]，使用哪些轨道参与动力学演化，设置的活性空间轨道为6和7。
params[“states”].append([“GS”,[6],0.00])，基态轨道为6，0.00可以作为剪刀算子将轨道能量升高或者降低，例如设置1代表将6轨道能量增加1 eV，设置-1为降低1 eV，一般在拟合实验带隙时使用。
params[“states”].append([“S1”,[7],0.00])，激发态轨道为7，其他同理。

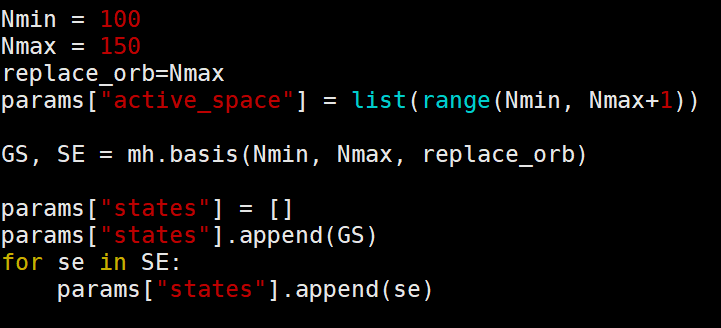
有时也可以写作上面的形式，这时一般考虑的是载流子弛豫而非复合，表示从第150个KS轨道一直向下演化到第100个轨道。

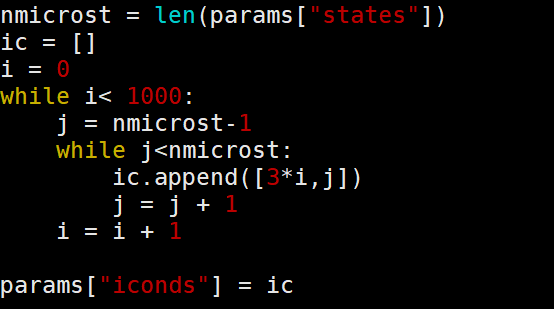
上图为如何生成初始条件。
while i< 1000表示生成1000条独立的随机轨迹来进行系综平均，这里采样的是核的热运动轨迹。
j = nmicrost-1表示最后一个电子态的索引，这里给的例子仅有0和1两个态，因此j被设置为1，表示最高激发态。
ic.append([3*i,j])表示间隔多少步选择核的位置和动量作为$t = 0$时刻，如果没有间隔，那么相邻两条轨迹的原子核构型太过相似，统计相关性太高。间隔选取3（0，3，6，9……）为了让轨迹的初始构型有足够差异。

上图为计算结束输出的载流子寿命，其中sh_pop_ex1是面跳跃的跃迁概率$P^{\rm SH}_k(t) = \frac{N_k(t)}{N}$，se_pop_ex1是薛定谔方程的跃迁概率$P^{\rm SE}_k(t) = |c_k(t)|^2$。二者没有固定大小关系。se_en_ex1和sh_en_ex1则是能量演变。

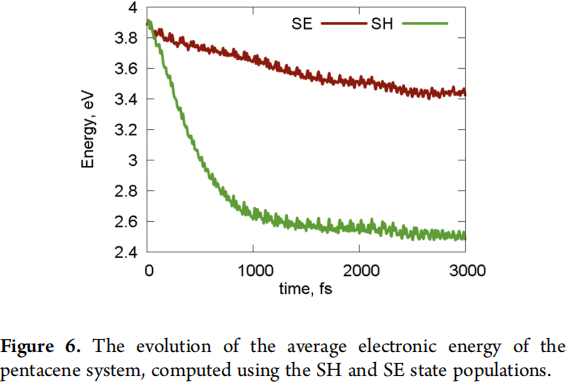
上图就为两种方式计算出的能量演变。

相位修正

实际的计算当中，非绝热耦合计算使用的是式（56）计算非绝热耦合，又写做下式：

其中，计算$t$时刻和$t+\Delta t$时刻的波函数相位不一定相同。因为对于不同相位并不会改变电子云的形状，也不会改变能量。如果有一个波函数 $|\psi\rangle$，它满足下式：

那么将波函数乘上任何一个相位因子 $e^{i\theta}$（其中 $\theta$ 是任意实数），下式依然成立：

因为电子出现的概率密度为 $P = |\psi|^2$。而又因为 $|e^{i\theta}|^2 = 1$，所以相位因子不会改变电子云的形状，也不会改变能量。
VASP在每个离子步独立对角化哈密顿量，每次得到的相位$\theta$是随机的。即使让VASP在算当前步的时候给了上一步的波函数做初猜，但是在自洽迭代的过程中，数值误差积累或者算法收敛路径上有差异，也会导致相位稍有不同。

例

• 1、简单的2能级系统，通过式（72）计算非绝热耦合，在没有相位差的情况下：
• $$\psi_1(t) = e^{i0.5\pi} \frac{1}{\sqrt{2}} (1, 1)$$
• $$\psi_2(t) = e^{i0.5\pi} \frac{1}{\sqrt{2}} (1, -1)$$
• 相位均为0.5，并且在下一个$t+dt$时刻相位保持不变：
• $$\psi_1(t+dt) = e^{i0.5\pi} \frac{1}{\sqrt{2}} (1.00, 0.98)$$
• $$\psi_2(t+dt) = e^{i0.5\pi} \frac{1}{\sqrt{2}} (0.98, -1.02)$$
• 注意：这里为方便计算前面没有将其归一化，实际上应该需要归一化处理再进行后续计算，但是目前主要问题是看相位不一致的情况下计算出的非绝热耦合，因此这里简化处理不进行归一化。
• 根据式（72），分别计算$S_{12} = \langle \psi_1(t) | \psi_2(t+dt) \rangle$和$S_{21} = \langle \psi_2(t) | \psi_1(t+dt) \rangle$
• 先计算第一项：
• $$\begin{aligned}S_{12} &= \left( e^{i0.5\pi} \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \right)^\dagger \cdot \left( e^{i0.5\pi} \frac{1}{\sqrt{2}} \begin{pmatrix} 0.98 \\ -1.02 \end{pmatrix} \right) \\&= \left( e^{-i0.5\pi} \frac{1}{\sqrt{2}} (1, 1) \right) \cdot \left( e^{i0.5\pi} \frac{1}{\sqrt{2}} \begin{pmatrix} 0.98 \\ -1.02 \end{pmatrix} \right) \\&= e^{-i0.5\pi} \cdot e^{i0.5\pi} \cdot \frac{1}{2} \cdot \left( 1\times 0.98 + 1 \times (-1.02) \right) \\&= \mathbf{-0.02}\end{aligned}$$ 注意：一般来说，求$\langle \psi_1(t) | \psi_2(t) \rangle$需要先将$\psi_1(t)$求复共轭后再求转置，取复共轭是满足量子力学要求，转置是为了满足线性代数的乘法要求，因此要将左矢求复共轭及转置。
• 同理，第二项可以计算出等于0.01。
• 因此，最后NAC计算结果为-0.03。
• 2、如果在下一个时刻$t+dt$时刻相位改变：
• $$\psi_1(t+dt) = e^{i0.3\pi} \frac{1}{\sqrt{2}} (1.00, 0.98)$$
• $$\psi_2(t+dt) = e^{i0.7\pi} \frac{1}{\sqrt{2}} (0.98, -1.02)$$
• 同样分别计算两项NAC数值。
• 先计算第一项：
• $$S_{12} = e^{i(0.52-0.3)\pi} (-0.02) = e^{i0.22\pi}(-0.02)$$
• $$e^{i0.22\pi} \approx \cos(39.6^\circ) + i\sin(39.6^\circ) \approx 0.77 + 0.64i$$
• 第一项计算为$-0.0154 - 0.0128i$
• 同理计算第二项为$0.0084 - 0.0054i$
• 因此，这时计算结果为$0.0238 - 0.0074i$

因此，如果不进行相位修正，计算出的不同相位会导致计算出的非绝热耦合会失去物理意义，实部从-0.03变成了-0.0238，出现了较大的误差，且出现了虚部，这是本不应该出现的数值噪声。

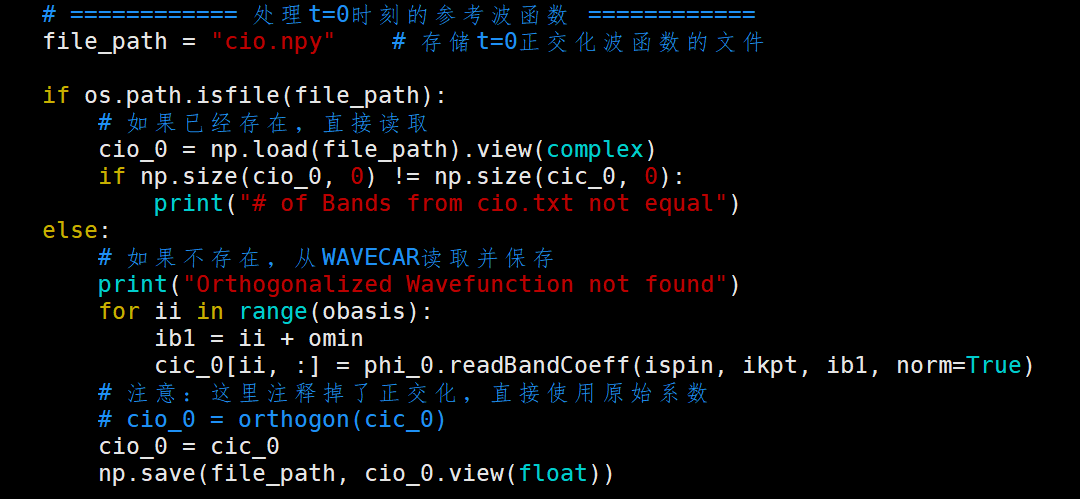
脚本先将$t=0$时刻的波函数$\psi_{ref}(0)$存储起来，而其中包含了随机相位因子 $e^{i\alpha}$，因此可以得到：

需要修正的$t$时刻波函数可以设置为$\psi_{now}(t)$，同样存在一个相位因子$e^{i\beta(t)}$，因此可以写作：

此时需要计算相对的相位因此，即计算重叠积分：

上式即为代码计算中对所有元素相乘并求和：
cor1 = cio_0.conj() * cio_t
cor1 =np.sum(cor1,axis=1)
为了得到$e^{i(\beta - \alpha)}$，还需要除以模长，即：

cc1 = cor1 / abs(cor1)
上式即为：

对原始的$\psi_{now}(t)$乘以$P^*$即可得到相修正完成后的$\psi_{corr}(t)$

可以看出尽管依然带有随机相位，但是此时的相位已经变成了$e^{i\alpha}$，内积中会全部抵消，因此相修正结束。
同理，对$t+dt$时刻的波函数进行修正即可。
以上便为相位修正的原理。

全电子校正

需要使用到的量子力学：

1、波函数假设

量子系统的状态由一个波函数 $\Psi(\mathbf{r}, t)$ 完全描述。

即波函数代表了在任何给定时间$t$时粒子的空间分布

统计诠释

其中，波函数的模平方给出粒子在位置 $\mathbf{r}$ 处出现的概率密度：

其中：

• $P(\mathbf{r}, t)$为在$t$时刻时候，在$r$位置发现粒子的概率
• $\Psi^(\mathbf{r}, t)$ 为$\Psi(\mathbf{r}, t)$的复共轭（取虚部相反，即$\bar{z} = a + bi$的复共轭为$\bar{z}^ = a - bi$）。

上式又称为波函数的统计诠释。 更精确一些表达：

表示了在$t$时刻发现粒子处于a和b之间的几率。

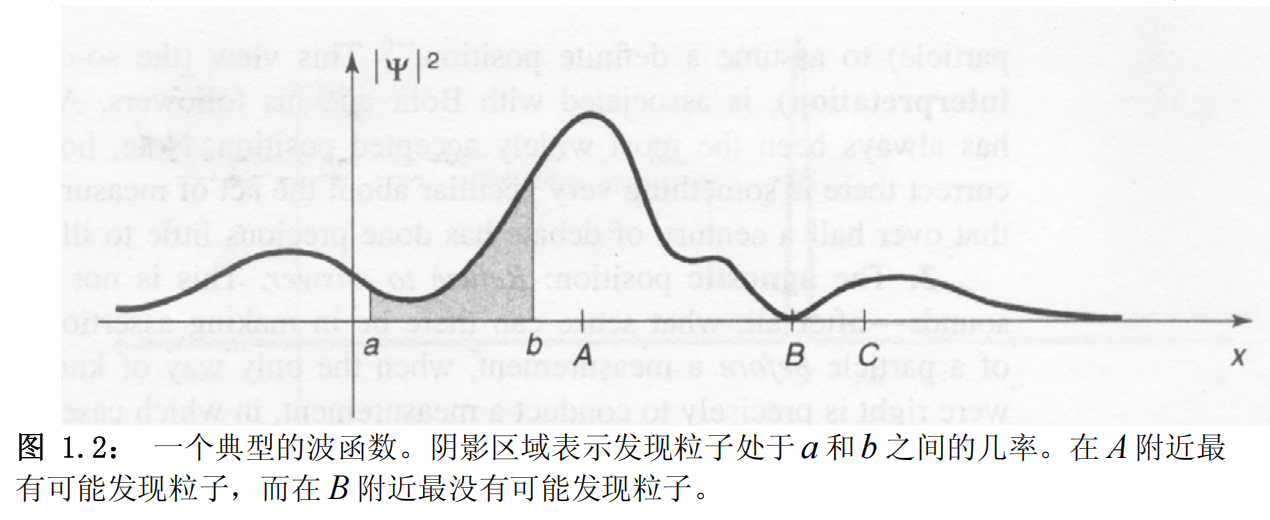
归一化条件

总概率必须为1：

即在整个空间中一定能找到可以由$\Psi$表示的粒子，在全空间中找到它的概率为1。

2、算符假设

每个可观测量对应一个厄米算符

物理可观测量（如位置、动量、能量等）都对应于希尔伯特空间中的一个线性厄米算符。
因为厄米算符保证了其本征值（测量结果）均为实数。

• 位置算符：$\hat{x} = x$
  
• 动量算符：$\hat{p} = -i\hbar \nabla$

本征值方程

其中 $a_n$ 是算符 $\hat{A}$ 的本征值，$\psi_n$ 是对应的本征态。

3、测量假设

对可观测量 $\hat{A}$ 的测量只能得到其本征值之一。

若系统处于状态 $\Psi$，测量得到本征值 $a_n$ 的概率为：

测量后，系统状态坍缩到对应的本征态：

4、薛定谔方程

薛定谔方程

系统随时间的演化由薛定谔方程描述：

其中 $\hat{H}$ 是哈密顿算符。

定态薛定谔方程

当势能与时间无关：

薛定谔方程写作：

5、全同粒子假设

交换对称性

全同粒子不可区分，波函数对于粒子交换必须具有确定的对称性。

• 玻色子：波函数对称
  
• $\Psi(\mathbf{r}_1, \mathbf{r}_2) = +\Psi(\mathbf{r}_2, \mathbf{r}_1)$
• 费米子：波函数反对称
  
• $\Psi(\mathbf{r}_1, \mathbf{r}_2) = -\Psi(\mathbf{r}_2, \mathbf{r}_1)$

泡利不相容原理

两个费米子不能处于相同的量子态。

参考文献

[1]、Molecular dynamics with electronic transitions, J. Chem. Phys. 1990, 93, 1061–1071. [2]、The PYXAID Program for Non-Adiabatic Molecular Dynamics in Condensed Matter Systems, J. Chem. Theory Comput. 2013, 9, 4959–4972. [3]、Advanced Capabilities of the PYXAID Program: Integration Schemes, Decoherence Effects， Multiexcitonic States, and Field-Matter Interaction, J. Chem. Theory Comput. 2014, 10, 789–804. [4]、Decoherence-induced surface hopping, J. Chem. Phys. 2012, 137, 22A545. [5]、量子力学概论，2009，Griffiths.